新しいマーケティングのすすめ（32）
「ヒット商品3.0と波動方程式」
目次
突然ですが、pythonと波動方程式の紹介
この連載を読んでいる方の中には、マーケティングで、データサイエンスを行なっており、そして、その中でプログラミングを行う人もいるでしょう。もし、プログラミングに慣れていなくても、少し私に騙されたと思って、以下のプログラミングのドアを開いてみましょう。
検索サイトで「Google Colab」と入力してみてください。おそらく、次のGoogle Collaboratoryというサイトを発見できるはずです。このサイトは、誰でもPythonというプログラムを学び、実行できる環境です。
このGoogle Colabの「ファイル」→「ノートブックを新規作成」を選べば、プログラムの入力画面が開きます。ここに、何も考えずに、以下のプログラム・コードを、コピー＆ペーストしてみてください。
—
import numpy as np
import matplotlib.pyplot as plt
# 波の振幅
A1 = 1
A2 = 1
# 波の位相
phi1 = 0
phi2 = np.pi
# 波のx座標
x = np.arange(-10, 10, 0.01)
# 各波の振幅と位相を加算して合成波の振幅と位相を計算する
y1 = A1 * np.sin(x * 2 * np.pi + phi1)
y2 = A2 * np.sin(x * 2 * np.pi + phi2)
y = y1 + y2
# y1のグラフを描画する
plt.plot(x, y1)
plt.show()
# y2のグラフを描画する
plt.plot(x, y2)
plt.show()
# 合成波のグラフを描画する
plt.plot(x, y)
plt.show()
—
そして、左上に▶️マークがあるので、それを押すことで、プログラムが実行され、以下3つのグラフが登場するはずです。
図1
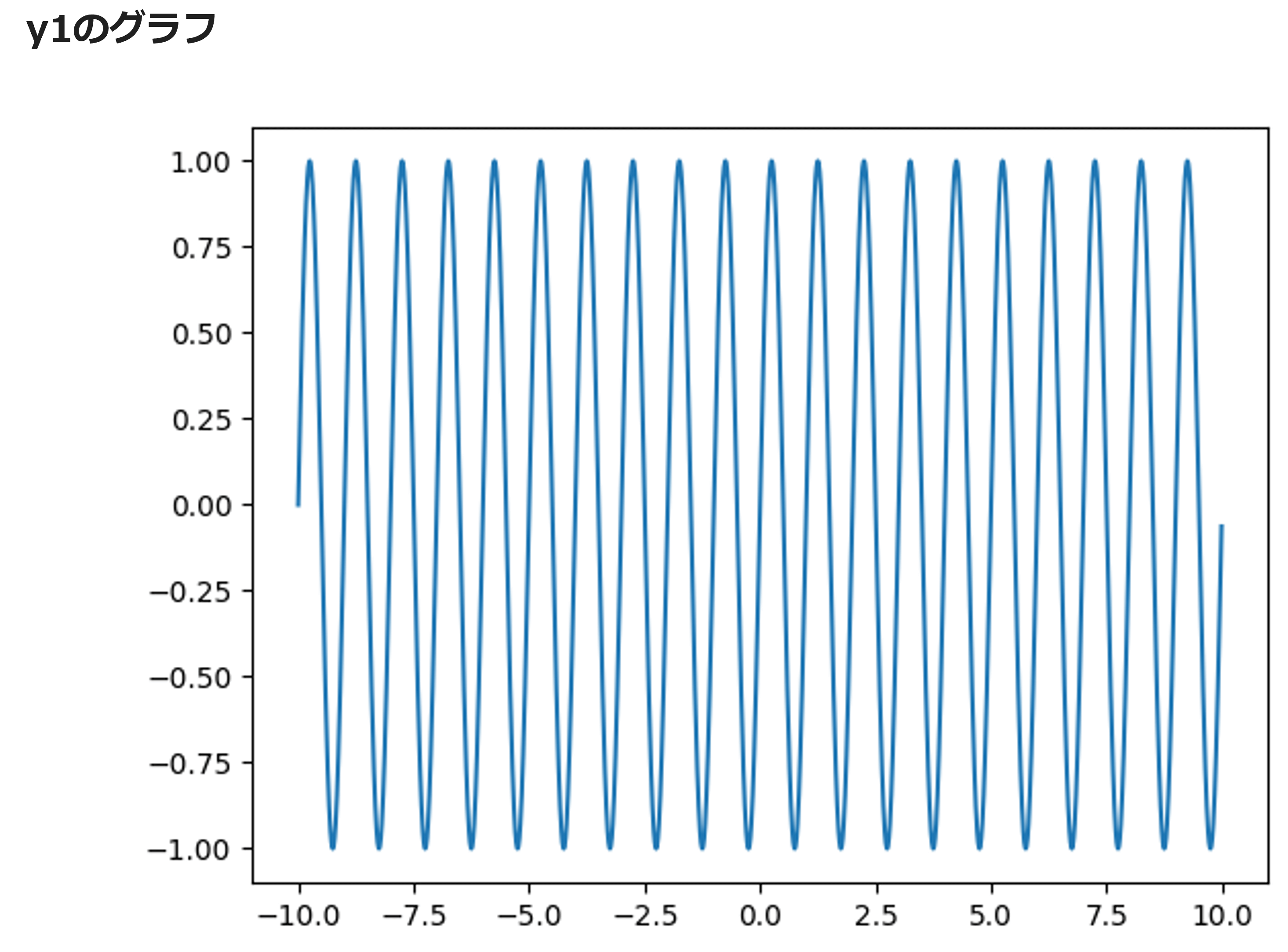
図2
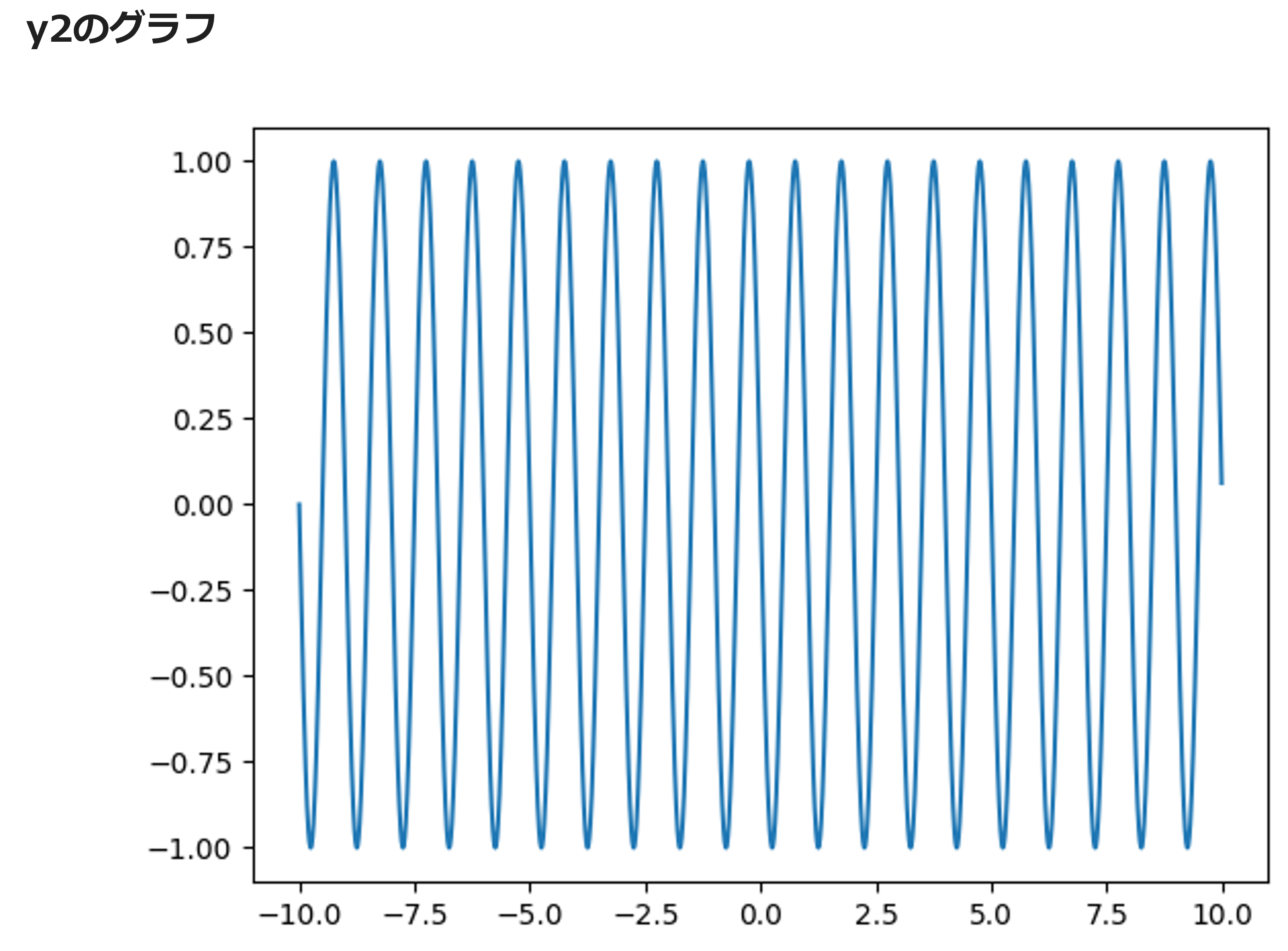
高校で物理を学んだ方には馴染みのある、波の合成の実験です。複雑なことは少し無視して、2つの単純な波動(y1,y2)を重ねると、重ね合わせは複雑な図3のようになります。
図3
マーケティングに波動方程式は関係あるのか
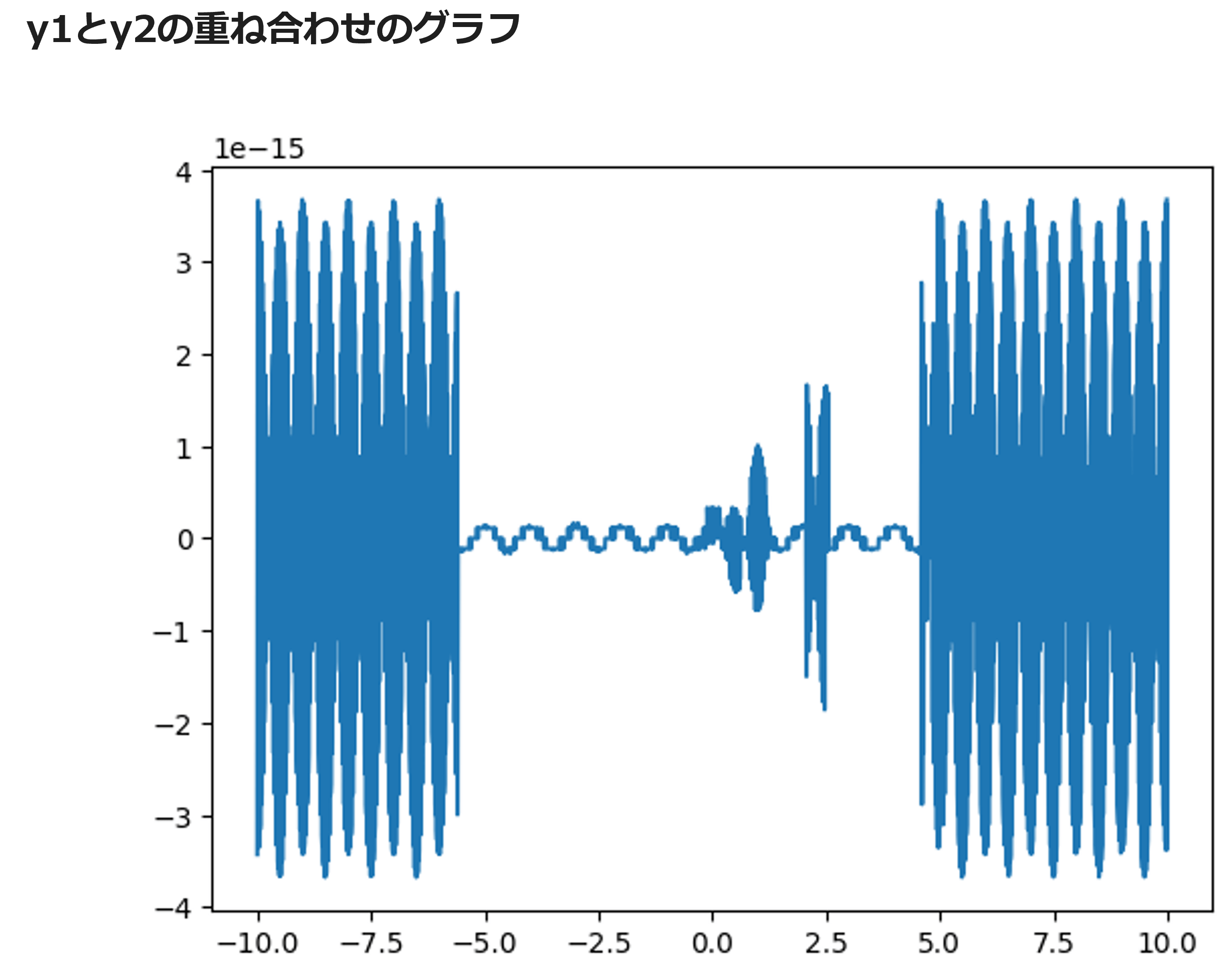
この波動方程式の、x軸を時間、y軸をあるグループでの商品の話題度としましょう。ここでは、y1をAグループにおける話題度、y2をBグループにおける話題度とします。そして、それぞれのグループのリズムで盛り上がりと落ち着き、互いへの影響を繰り返した結果、AグループとBグループは、SNSで相互に繋がっていたとすると、AとBグループ全体の話題の挙動は、先ほど書いた重ね合わせの図3のグラフになります。（理想的な状況では。）
この話は、前回の記事「ヒットの定義」の続きです。前回、ヒット商品3.0の定義を紹介しました。ヒット商品3.0では、SNSがマーケティングに大きく関係していて、このSNSの話題を考えるときに、多くのマーケッターは、SNSの記事の出現や、「いいね」などのエンゲージメントを表す代表値を測定しています。しかし、その背景にある、SNSのメカニズムは理解しているでしょうか？
多くのマーケティングの現場では、SNS空間で、商品とお客様の関係には注目しています。Xで何人にポストが伝わったとか、Instagramの写真が何人に見られたかなどです。しかし、SNSでは、個人と個人の関係が重要で、この波動のシミュレーションのように、個人間の影響も存在します。しかも、この2つのグループA,Bのように、話題になる時期がずれることもあります。実は、このような関係も、マーケティングと一見関係なさそうな、「物理」の知識を使うと、解明できるかもしれないのです。
ヒット商品1.0時代とヒット商品3.0時代では、マーケティングのメカニズムが大きく異なる
ヒット商品1.0時代は、マーケティングに大きく影響を与えているのは、マーケティング・コミュニケーションで、その主役は、テレビ広告に代表されている、広告・宣伝でした。そのため、ヒット商品1.0時代には、広告の到達量（リーチ）と広告接触回数（フリークエンシー）を重要な指標としていました。
SNSが重要なヒット商品3.0時代、私たちマーケターは、SNSの発言も広告・宣伝のリーチとフリークエンシーで考えていないでしょうか？SNSには、SNS参加者の相互作用があり、その相互作用は、リーチ、フリークエンシーでは説明できないでしょう。しかし、今でも多くのSNSの関係者が、総発言数や、総エンゲージメント数を、単純足し算で測定して、説明しようとしています。
SNSは、時系列変化が重要で、単純なある期間の総話では説明できないことが多いでしょう。今回、私が大胆に仮説として提示した、波動方程式のような新しい説明モデルが必要なのでしょう。
データサイエンスと合わせて行いたい、数値実験
ここ数年、企業のマーケティングではデータサイエンスに焦点があたっています。それは、今後も続くと思います。今回私が提案したいのは、今回の記事のような「数値実験」をもっとマーケティングに持ちこむことの重要さです。マーケットの挙動を説明する数式やモデルを考え、コンピューターで計算し、現状をどれだけ説明しているかというアプローチです。
マーケットは絶えず進化します。それに対応するために、マーケターは、マーケットで起きていることの理解を行う必要が永遠に続くでしょう。その一つの武器にマーケティングの理解のための「数値実験」があるのかもしれません。
著者プロフィール
転載・引用について
◆本レポートの著作権は、株式会社インテージが保有します。
下記の禁止事項・注意点を確認の上、転載・引用の際は出典を明記ください 。
「出典：インテージ 「知るギャラリー」●年●月●日公開記事」
◆禁止事項：
・内容の一部または全部の改変
・内容の一部または全部の販売・出版
・公序良俗に反する利用や違法行為につながる利用
・企業・商品・サービスの宣伝・販促を目的としたパネルデータ（＊）の転載・引用
（＊パネルデータ：「SRI＋」「SCI」「SLI」「キッチンダイアリー」「Car-kit」「MAT-kit」「Media Gauge」「i-SSP」など）
◆その他注意点：
・本レポートを利用することにより生じたいかなるトラブル、損失、損害等について、当社は一切の責任を負いません
・この利用ルールは、著作権法上認められている引用などの利用について、制限するものではありません
◆転載・引用についてのお問い合わせはこちら
